
Pensando sobre tecnología en la clase de matemáticas
https://eduteka.icesi.edu.co/articulos/Tema19
PENSANDO (Y HABLANDO) SOBRE TECNOLOGÍA EN LA CLASE DE MATEMÁTICAS
Por: Paul Goldenberg, Centro para el Desarrollo de la Educación.
Actualmente, una de las tendencias más fuertes en el crecimiento y evolución de las matemáticas y su enseñanza, está dada por el poder de las nuevas tecnologías (TICs). En matemáticas, los computadores han generado campos enteramente nuevos. En educación han resaltado la importancia de algunas ideas, posibilitado el acceso a ciertos tópicos y problemas y ofrecido nuevas maneras de representar y manipular información matemática, haciendo posible escogencias sobre contenido y pedagogía que nunca antes se habían tenido.
Pero estas escogencias llevan con ellas la carga de realizar juicios. No todo lo que puede hacerse debe hacerse. El aprendizaje del estudiante se ve afectado por un sistema complejo: maestros, teorías educativas y creencias, padres, currículos, intereses del estudiante, expectativas culturales, tecnología y otras. Mucho es lo que hay para decir sobre las anteriores consideraciones, pero el impacto de cada una no puede entenderse a cabalidad sino en relación con las demás. Esto es especialmente cierto en lo referente a tecnología, lo que en parte explica por qué no existe una visión única, universalmente aceptada de cuál es la mejor forma de utilizar las calculadoras y los computadores en el aula de clase.
Es más, las preguntas adecuadas sobre tecnología no son sobre temas amplios como qué hardware o software utilizar, sino desde cómo cada uno funciona en un determinado currículo hasta los efectos que tienen en la forma de plantear problemas particulares a los estudiantes. Para cada caso único, se debe juzgar si el uso de la tecnología es efectivo y apropiado o no. La necesidad de tomar decisiones en ese nivel de detalle no debe sorprendernos si pensamos en las calculadoras y los computadores de la misma forma en que lo hacemos sobre los lápices. Son los problemas que se plantean, no la tecnología con la que se encaran, lo que hace la diferencia. Con computadores o con lápices, algunos problemas son excelentes y otros son pérdida de tiempo.
Lo que cambia con la tecnología es el conjunto de problemas entre los que se puede escoger y la forma en que se pueden presentar. Algunos son muy difíciles de plantear en las aulas que utilizan únicamente lápices. Ciertas lecciones requieren que los estudiantes experimenten con objetos matemáticos y observen cómo responden. Algunas requieren representaciones visuales (gráficas, diagramas, figuras geométricas, imágenes en movimiento) para responder a los interrogantes, órdenes o respuestas de los estudiantes.
En los grados de Básica primaria, elementos físicos manipulables con frecuencia ofrecen a los niños este apoyo visual y experimental. Sirven como soportes temporales de ideas matemáticas, objetos que los niños pueden ver y manipular con sus propios ojos y manos, mientras aprenden a ver y manipular mentalmente ideas matemáticas. En los grados superiores muchas ideas matemáticas no cuentan con esos modelos físicos. Los computadores, pueden ofrecer "manipulables virtuales" interactivos, cuando los elementos físicos no existen. Como siempre, el valor de una herramienta depende del uso que se le dé. Si los manipulables físicos o electrónicos están bien diseñados y se utilizan adecuadamente, pueden incrementar la cantidad de problemas que pueden pensar y resolver los estudiantes.
¿Pero qué es buen uso? La investigación responde parcialmente la pregunta, pero no ofrece toda la respuesta. Esto obedece a una razón, los objetivos difieren de una institución a otra y aún difieren entre aulas de clase. La claridad sobre los objetivos y el buen juicio del maestro son componentes necesarios de las decisiones que se tomen sobre la utilización de cualquier método de enseñanza. Este artículo pretende ayudar a los maestros a decidir cuándo, cómo y dónde hacer uso de computadores o calculadoras y, cómo maximizar las ganancias y minimizar los riesgos de hacerlo. Pretende además, ofrecerles estrategias para hablar con los padres de familia sobre esas escogencias.
ALGUNAS FORMAS DE DECIDIR QUÉ ES BUEN USO:
Lo más importante que han señalado las investigaciones es que lo importante realmente no es hacer uso de la tecnología sino cómo hacerlo (aunque esto parece obvio para los maestros, no es esta la manera cómo se debate públicamente). A pesar de las investigaciones, ningún documento puede pronunciarse con seguridad sobre lo que es buena o mala práctica, porque mucho sigue siendo juicio personal o de la comunidad. Pese a lo anterior parece haber acuerdo suficiente, entre los amantes de la tecnología y los que la detestan, sobre algunos principios razonables que pueden ayudar a que el maestro tome sus propias decisiones. A continuación se exponen 6 de estos principios que ayudan a reflexionar sobre el uso de la tecnología en las clases de matemáticas. Todos apuntan a la necesidad de examinar el propósito de la lección; esto es, la naturaleza de las necesidades actuales de los estudiantes y de qué manera encaja la tecnología dentro de ese propósito.
Mientras el currículo es el determinante real de cuáles son las ideas matemáticas que ganan los estudiantes, desde la perspectiva de ofrecerles ambientes matemáticos ricos dentro de los que encuentren, representen, experimenten y razonen sobre ideas matemáticas, por lo general los computadores ofrecen mayor versatilidad que las calculadoras. Enfocándonos solamente en el espacio del monitor éste hace posible un rango mayor de ideas matemáticas, con más formas para representarlas y manipularlas. Esa versatilidad también acomoda mayor variedad de estilos de enseñanza y aprendizaje pues ofrece escenarios educativos como: rompecabezas, micromundos (ambientes específicamente diseñados para educación pero parecidos en su estructura a herramientas), tutoriales, ambientes de programación matemática, visualizaciones en dominios matemáticos desde estadística hasta cálculo, herramientas de construcción geométrica y más.
No obstante la variedad, fidelidad y poder matemáticos además del valor educativo de muchas herramientas del computador, razones económicas y de otros tipos han llevado las calculadoras a colegios y currículos en una escala que hasta ahora no han alcanzado los computadores. Por eso la controversia de la tecnología en las aulas de matemáticas se enfoca primordialmente en éstas. El énfasis de este documento será proporcional no a las oportunidades que parecen mucho mayores con el computador, sino a las actuales realidades de las aulas de clase en las que las calculadoras, al menos por el momento, dominan.
"HABILIDADES DE ORDEN SUPERIOR" O "HABILIDADES DE ORDEN INFERIOR"
ESCOGENCIA DE UN TIPO DE TECNOLOGÍA
Un reporte de fácil lectura del Servicio de Evaluación Educativa de 1998 (ETS, por su sigla en inglés) esboza el debate sobre la efectividad de la tecnología y concluye que el uso de computadores para enseñar habilidades de orden superior como interpretar, razonar y resolver problemas, estaba "positivamente relacionado al logro académico en matemáticas y al ambiente social de la escuela". Además, "usar los computadores para enseñar habilidades de orden inferior (como aprender hechos y datos) estaba negativamente relacionado" a las mismas variables. Muestra también que la naturaleza, no la frecuencia, del uso en la escuela era factor crítico.
Muchas personas aceptan que es necesario aprender datos; anótese que el estudio ETS atribuye efecto negativo no al aprendizaje de datos, sino al uso de la tecnología para lograrlo. Y la mayoría de los maestros acepta que desarrollar acceso rápido y fácil a hechos y datos útiles (que a veces se llama fluidez) requiere práctica. Los juegos de computador se usan a veces para ofrecer práctica sin la monotonía que con frecuencia tienen para los estudiantes las hojas de trabajo. Pero aunque tengan algún valor del tipo de motivación u otro para esa práctica, aparentemente no son el camino a seguir. No especifica la investigación por qué los computadores en apoyo de las habilidades de orden inferior tienen efecto negativo, por lo que no podemos deducir un principio general diferente a no usar los computadores para actividades repetitivas.
¿Qué significa realmente la diferencia entre utilizar herramientas para habilidades de orden superior o inferior? La respuesta involucra varios factores. Algunos de ellos son la consideración de que lo que en un momento dado es pensamiento de orden superior se convierte en orden inferior en una etapa posterior, por lo que el nivel de desarrollo de los estudiantes y su experiencia matemática previa hacen parte del cuadro. Además, la naturaleza del problema tiene importancia: si se paga un artículo de $75 con un billete de $100, hay que pensar más si se pregunta, de cuantas formas se puede entregar el cambio, que si se pregunta qué cambio dar.
También la tecnología tiene importancia. Los estudiantes están en una situación diferente cuando el software les plantea problemas que deben resolver (tutoriales, software de práctica y muchos juegos son así) a cuando el software espera que el estudiante formule y resuelva el problema. Los procesadores de texto esperan en blanco, a que el escritor tenga ideas, y a que las exprese, desarrolle y edite. El trabajo real lo hace el escritor. De la misma forma, existen ambientes matemáticos, que en su conjunto podrían denominarse "procesadores de ideas matemáticas", que también esperan que el estudiante matemático produzca ideas, las exprese, desarrolle y edite. Estas incluyen lenguajes de programación, software dinámico para Geometría del tipo "Geometer's Sketchpad y Cabri", hojas de cálculo, calculadoras de álgebra simbólica, y otros similares. Como en una buena clase de escritura, el maestro y el currículo juegan un papel central: los estudiantes no "tienen" simplemente ideas, necesitan buenos problemas para trabajar, algunas habilidades y formas de pensar, desarrollar un arsenal de estrategias y técnicas, hechos, y dirección. Pero con los "procesadores de ideas" como con los procesadores de texto, hojas de cálculo, lenguajes de programación, y software de construcción para geometría [1] y, con algunos micromundos especialmente diseñados con fines educativos (el programa de estadísticas Fathom [2] por ejemplo) el maestro y el currículo pueden controlar la calidad de los problemas, y no el diseñador del software. Es más, el enfoque a la solución de problemas puede estar bajo el control del estudiante, con dirección del maestro.
¿Es el procesamiento de ideas el único uso recomendable de la tecnología? No. Mientras el estudio ETS alerta sobre el enfoque de la práctica de habilidades de orden inferior, algunos rompecabezas y juegos brillantes, se enfocan claramente en el pensamiento de orden superior, aunque plantean el problema y dejan a los muchachos únicamente resolverlos. Y para algunos estudiantes, en determinadas circunstancias, el software que ofrece práctica con habilidades aritméticas elementales tiene un papel.
|
EL PRINCIPIO DE GÉNERO: La toma de buenas decisiones requiere que los maestros estén conscientes de los diferentes papeles que puede jugar la tecnología; se debe pensar claramente cuáles son las metas de las clases, y las necesidades particulares de estudiantes específicos; y escoger las tecnologías que directamente promuevan esos objetivos, en lugar de simplemente involucrar tecnología en el aula de maneras que pueden ser atractivas pero cuyos resultados sean tangenciales y aún perjudiciales para las metas establecidas. |
REFLEXIONE SOBRE EL PROPÓSITO DE LA LECCIÓN
Por supuesto que lo que enreda a los estudiantes en los detalles de los cálculos, depende no solamente de la cantidad de éstos, sino de lo que el estudiante considera fácil de hacer, así que de todos modos se requiere juicio. Para los niños de 6 años predecir cuantas pulgadas hay en 20 pies, puede ser un excelente problema para estimar sin usar calculadora. Por otra parte puede ser un paso difícil y convertirse en distracción en un proceso en el que otro de los pasos es el núcleo de la lección. En este caso el uso de calculadoras se puede autorizar. Cuando los alumnos tienen 10 años deben estar en capacidad de multiplicar mentalmente 12 x 20 así que hacer uso de la calculadora no constituye desvío de la lección, así no sea este el punto de la clase.
Lo que irrita a las personas es el hábito que desarrollan algunos estudiantes de usar las calculadoras para dividir por 10 o por 100, u otro tipo de cálculos que todo el mundo puede realizar mentalmente. Con muy pocas y extraordinarias excepciones, hay personas que necesitan usar la calculadora en estos casos. Ellas han sido lesionadas por una mala educación y no por una limitación de su habilidad "innata".
|
EL PRINCIPIO DEL PROPÓSITO: Permita el uso de calculadoras cuando la tarea de hacer cálculos pueda interferir con el propósito de la lección. Cuando aprender a realizar los cálculos es el propósito de la lección, las calculadoras son una mala idea. |
PIENSE EN LA NATURALEZA DEL PENSAMIENTO QUE SE LES PIDE A LOS ESTUDIANTES
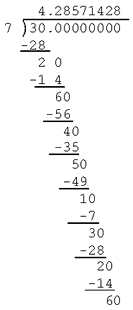
7 cabe 2 veces en 20 y sobran 6.
Después de unos pocos pasos más nos encontramos nuevamente con que "7 cabe 4 veces en 30"
¿Por qué? Por que se ha llegado a un punto en el que no hay ningún residuo (y los decimales se acaban) o queda un residuo. Como solamente existen seis residuos posibles, en alguna forma se deben repetir. Cuando lo hacen, un 0 (cero) que hemos bajado comienza un proceso ya visto. Los residuos deben completar un ciclo y así los dígitos del cuociente se repiten.
Aunque el ejemplo es solamente sobre 7 y 30, el razonamiento es el general, no depende en absoluto de los números seleccionados. En cada paso de la división, o no hay residuo y el decimal termina, o queda un residuo. Cuando se divide por n, el residuo debe ser menor que n. Si no hay residuo esto es, si el residuo es 0, la división termina. Por lo tanto solamente son posibles n-1 residuos diferentes a 0. Cuando la división prosigue, solo se "bajan" ceros, de tal manera que un máximo de n-1 números diferentes (todos múltiplos de 10) serán divididos por n. Por lo tanto en un máximo de n-1 pasos, el proceso debe o terminar o repetir la división que se efectuó antes con exactamente los mismos pasos sucesivos, un ciclo que se repite.
Debido a que el apoyo en los cálculos puede facilitar el trabajo de obtener resultados iniciales y reducir errores molestos que pueden oscurecer el patrón, éste puede ser útil en el momento en que los estudiantes estén estableciendo una hipótesis. Pero entender la razón para que se produzca el patrón puede requerir que realicen el algoritmo de la división por lo menos una vez para ver los resultados intermedios. En este momento la calculadora no es ayuda sino estorbo.
|
PRINCIPIO DE RESPUESTA VERSUS ANÁLISIS: El Principio del Propósito decía que usar la calculadora era admisible si el propósito de la lección se alcanzaba mejor cuando se llegaba rápidamente a la respuesta en lugar de trabajarle por largo rato o distraerse con los cálculos. Otras veces, aún cuando el proceso de calcular no constituye el objeto de la lección, realizar ese proceso y ver los detalles intermedios explica los resultados que se producen. En este caso, una tecnología que no deje ver los detalles y produzca directamente el resultado, no ayuda. |
También te podría interesar
El Pensamiento Crítico, más allá del Procesador de Texto
Ver artículoCómo aprende la gente (Primer Capítulo)
Ver artículoLa Integración de las TIC en Ciencias Naturales
Ver artículoDeclaración de la NCTM sobre el uso de la tecnología
Ver artículoREFLEXIONE SOBRE EL PAPEL DE LA TECNOLOGÍA EN LA LECCIÓN O ACTIVIDAD
0.3 x 10 = 3 x 0.1 x 10 = 3 x 1/10 x 10 = 3 x 1 = 3
o quizá presentar el razonamiento tal como es, puramente simbólico. O se puede recurrir a solicitar consistencia en la notación: si cinco dieces se escribe 50, y nueve dieces 90, entonces treinta y seis dieces debe escribirse 360, y 4.3 dieces debe estar entre cuatro y cinco dieces (con algunos detalles que se deben trabajar cómo en el caso de 0.3 x 10).
Nuevamente una representación visual puede ayudar, y ésta puede ser electrónica e interactiva, pero una herramienta para obtener la respuesta no es lo que se necesita.
La misma verdad aplica en álgebra. Los estudiantes deben investigar y luego hacer hipótesis sobre un patrón de cálculos algebraicos, usando la calculadora o el computador para facilitar el trabajo de llevar a cabo la manipulación simbólica. La tecnología puede mostrarles, por ejemplo, que:
Experimentos posteriores pueden sugerir un patrón, pero cómo se aprende que significa ese patrón. Una calculadora simplemente da la respuesta; la inferencia y la comprensión subyacen en los pasos intermedios que se realizan multiplicando manualmente. Éstos se pierden completamente si solamente se observan los resultados finales que producen las máquinas.
Esta es una forma de escribir de qué manera se ven los resultados cuándo los cálculos se hacen manualmente.
Esto parte el cálculo en dos partes, multiplicar por X y multiplicar por -1. Aunque hacerle seguimiento a los cálculos pueda requerir un componente manual, el trabajo real es enteramente mental, y los requerimientos mentales son absolutamente básicos para alcanzar un entendimiento mínimo de álgebra. Los estudiantes deben saber (y tener una confortable fluidez con) el efecto de multiplicar por -1 y el efecto de multiplicar por X. Los pasos siguientes son claros. Multiplicar por X da
Y multiplicar por -1 da
La suma de estas dos expresiones elimina la mayoría de los términos y deja solamente X5-1.
Aunque esto es únicamente un cálculo; y se dice permanentemente que la prueba no debe basarse en un solo ejemplo; es inmediatamente claro que la forma en la que funciona este ejemplo es suficientemente general para mostrar de qué manera, cualquiera de estos cálculos funciona, y probar la hipótesis del patrón. No usar máquinas ayuda.
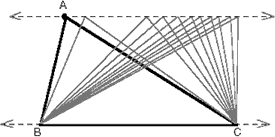
Por contraste, "The Teaching Gap" [4] y el video relacionado del Tercer Estudio de Ciencias y Matemáticas (TIMSS) [5] dan un ejemplo excelente de la forma en que una imagen dinámica, disponible con la tecnología, apoya la solución de problemas por parte de los estudiantes. Al resumir la lección anterior sobre Área de los Triángulos, un profesor muestra a sus estudiantes de 8º grado la imagen interactiva de un triángulo cuya base reposa fija en una de las dos líneas paralelas y su vértice reposa en la otra. A medida que mueve el vértice (A) adelante y atrás, destaca que la base permanece fija y la altura no cambia, y llama la atención de que por consiguiente, todos esos triángulos deben tener la misma área.
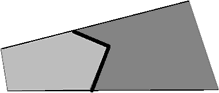
El maestro continúa con un nuevo problema para el día de hoy, lo presenta a la clase para que se trabaje independientemente sin instrucciones de cómo hacerlo. "El lindero entre la tierra de dos granjeros (línea oscura en la ilustración inferior) es quebrado, y ambos quieren enderezarlo, conservando cada uno la cantidad de tierra que actualmente tiene. Solucióneles el problema".
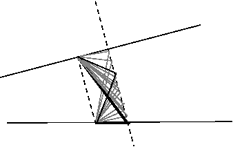
Aparecen varias soluciones. Algunos estudiantes recuerdan la imagen de un triángulo limitado por dos líneas paralelas y se dan cuenta de como lo pueden usar en este problema. Ellos ven el lindero como los dos lados de un triángulo, dibujan una paralela para el tercer lado por el vértice, y ajustan la figura (deslizando el vértice a lo largo de esa paralela hasta el final de uno de los lados) para solucionar el problema. En este caso, la imagen es una demostración manipulada por el profesor, pero herramientas como Geometer's Sketchpad y Cabri ofrecen "manipulables" que se ajustan por edad y contenido, y que permiten a estudiantes de Básica y Media realizar independientemente experimentos de ese tipo.
Herramientas geométricas, hojas de cálculo, calculadoras simbólicas, y herramientas para graficar pueden usarse para resolver problemas, pero su valor en ese papel es efímero: al paso del tiempo, la tecnología cambia y los estudiantes no podrán ya utilizar esas herramientas particulares. Con otra perspectiva (ayudar a los estudiantes a desarrollar formas nuevas y poderosas de enfocar los problemas, ayudarles a construir modelos mentales, a adquirir habilidades generalizables y flexibles, etc.) estas herramientas pueden promover aprendizaje que no se evapore con el desarrollo de nuevos productos. Los estudiantes que observan cuidadosamente cuando arrastran y distorsionan objetos en la pantalla, comienzan a aprender como realizar en sus mentes los mismos experimentos.
Aún para los estudiantes de Básica Primaria que trabajan con simples calculadoras aritméticas, existen actividades como "calculadora rota", que ayudan a que los estudiantes se enfoquen en y analicen la estructura y elementos de aritmética y adquieran habilidades a medida que entienden, en lugar de que la calculadora reemplace su pensamiento. Las actividades de "calculadora rota" [6] son en esencia rompecabezas en los que los estudiantes deben imaginar cómo realizar algunas tareas en una calculadora que tiene una o varias teclas que no funcionan. En diferentes niveles del aprendizaje de aritmética, problemas como "¿Cómo se puede multiplicar 20 x 50 si la tecla del O no está funcionando?" o "¿Cómo se puede multiplicar 5 x 12 si las únicas teclas numéricas que funcionan son el 5 y el 7?" o "¿Cómo obtener 6 como resultado en la calculadora si la única tecla numérica que funciona es el 5?" pueden ser retadores, divertidos e instructivos.
|
EL PRINCIPIO DE QUIÉN ES EL QUE PIENSA: El principio de la Respuesta versus el Análisis cuestiona si la tecnología se está utilizando para resolver problemas o para ayudar a los estudiantes a pensar sobre ellos, analizar los procedimientos, generar pruebas. De manera más general debemos preguntar, en relación específica a una lección o problema particular: ¿el papel de la tecnología es reemplazar una capacidad que el estudiante debería de alguna manera desarrollar? o ¿desarrollar la capacidad del estudiante para pensar, independientemente de la tecnología? Algo de cada una de estas dos opciones debe permitirse; pero el buen uso de la tecnología depende de tomar estas decisiones conscientemente. Este enfoque le ayuda a los estudiantes a desarrollar distintas maneras de pensar acerca de un problema, pensamiento que eventualmente llega a independizarse de la tecnología, lo que recuerda la conclusión del reporte ETS, de que usar la tecnología para enseñar habilidades de pensamiento de orden superior se relacionaba positivamente al logro matemático, mientras que usarla para promover habilidades de orden inferior se relacionaba negativamente. |
MANTENER EL CONTROL DEL CONTENIDO
Hasta hace poco tiempo, no había alternativa; las personas necesitaban el algoritmo de división para obtener respuestas exactas a problemas de división. Las cosas han cambiado. Encontrar cuocientes con precisión lo único que requiere hoy día es una calculadora: esa función para el algoritmo de división es obsoleta. Utilizar mucho del tiempo de la escuela luchando contra estas realidades parece elección equivocada. Pero ya se ha visto que pueden existir otras razones para aprender el algoritmo. De hecho, decidir si se debe enseñar no parece obvio; las personas razonables pueden llegar a conclusiones diferentes.
En los días en que se debía enseñar el algoritmo de división, no se preguntaba si existían otros propósitos que se beneficiaran con él, ya hemos visto uno. El método corriente de división constituye también una buena experiencia inicial con procesos infinitos y un ejemplo excelente de aproximación sistemática y refinamiento sucesivo. Así como la tecnología es solamente uno de los elementos de un complejo sistema interdependiente de factores que incluyen la enseñanza, los estudiantes y demás; ideas como la del algoritmo de división están completamente interrelacionadas con otras ideas matemáticas. Sacar una idea del currículo puede acarrear consecuencias inesperadas. No es un caso de conservar per se. Es importante reconsiderar las viejas prácticas, y algunas veces es necesario desechar contenido tradicional para abrirle campo a nuevas ideas. Pero?.
|
EL PRINCIPIO DEL CAMBIO DE CONTENIDO CUIDADOSO: Las decisiones sobre el contenido que está o no obsoleto, se deben hacer en forma reflexiva, teniendo no solamente en cuenta lo que la tecnología puede hacer, sino realizando un cuidadoso análisis de lo que los estudiantes deben estar en capacidad de hacer; especialmente de qué manera deben ser capaces de razonar. |
APRENDER A SER USUARIOS PODEROSOS DE TECNOLOGÍA
Pero el empoderamiento requiere control. Si los estudiantes no dominaban las viejas herramientas, no tiene objeto darles herramientas nuevas que tampoco dominen. En algunos casos los estudiantes saben suficiente álgebra para resolver un problema pero fallan en usar ese conocimiento porque carecen de la fluidez o experiencia para usarlo en forma efectiva y segura para resolver problemas. Esto mismo se aplica a las herramientas electrónicas. Aprender solo lo necesario sobre hojas de cálculo para resolver una clase de problemas específica; moverse luego a aprender un poco sobre herramientas de construcción de software de geometría para explicar un conjunto particular de temas geométricos, y pasar luego a otro tema, deja a los estudiantes cojos en el uso de éstas, no como expertos que pueden recurrir a las herramientas cuando las necesitan para ayudarles en el razonamiento y la solución de un problema.
Cuando las escuelas hacen planes para usar la tecnología, ellas desean como con cualquier currículo; hacer una aproximación gradual en el uso de herramientas, una aproximación que escoja un número limitado de herramientas, las presente en los primeros años y las utilice consistentemente, incrementando progresivamente el dominio y la sofisticación a lo largo de los años para que en últimas, los estudiantes se conviertan en usuarios poderosos de ellas para todo su aprendizaje matemático. Por supuesto, el currículo de matemáticas debe ser eso, de matemáticas, no de electrónica. En un aula de clase equipada con tecnología, como en una de lápiz y papel, la calidad reposa principalmente en qué tanto y qué tan bien están aprendiendo los estudiantes a pensar matemáticamente, pero el uso efectivo de la tecnología disponible (pulpa de papel o electrónica) también importa. Con el papel, la limpieza y el orden son importantes, como lo puede atestiguar cualquiera que haya visto los errores que cometen los estudiantes porque no pueden descifrar su propia escritura. Con las herramientas electrónicas se requieren otras habilidades. Debemos reflexionar sobre cuáles son las habilidades que deben desarrollar los estudiantes para usar de manera fluida y efectiva las nuevas herramientas a su disposición.
También se debe proveer tiempo y oportunidades a los maestros para que sean competentes con las herramientas, para que sean flexibles, puedan hacer juicios rápidos en sus clases sin sentirse constreñidos por las herramientas o frenados por su falta de seguridad en utilizarlas. Esta fue una de las conclusiones principales aunque no sorprendente, del Reporte ETS: el desarrollo profesional de los maestros en tecnología (a lo que nosotros agregamos: especialmente en lo que se refiere a las herramientas que apoyan el desarrollo de habilidades de pensamiento de orden superior) es extremadamente importante.
|
EL PRINCIPIO DEL USO FLUIDO DE LAS HERRAMIENTAS: "Manipular" varias de las herramientas de la calculadora o del computador, pero no dominarlas, puede producir más daño que beneficio: consume mucho tiempo y enseña poco. Aprender sobre pocas herramientas, pero a fondo, para utilizarlas concienzuda, inteligente, matemática, confiada, y adecuadamente para resolver problemas que son difíciles, realiza una contribución genuina a la educación matemática de los estudiantes. |
MANTENER EL APRENDIZAJE COMO PRIORIDAD
A MEDIDA QUE EL CAMBIO CONTINÚA SU MARCHA (INEXORABLE)
Es difícil resistir las gangas. Con la tecnología duplicando su capacidad y reduciendo sus costos a la mitad cada dos años, toda la sociedad parece arrastrada, seducida por las posibilidades y llevada por el impulso, y se mantiene difícilmente el equilibrio.
La primera ola de computadores que adquirieron las escuelas descansa en los armarios. Esto es suficientemente ilustrativo para indicarnos que el empuje inicial de la tecnología, en su mayor parte, no provino de las aulas de clase. Las escuelas constituyen un mercado muy grande, y la tendencia de mantenerlas tecnológicamente "al día" sirve los intereses económicos de los productores de hardware, software, y de los proveedores de acceso a Internet. Las políticas, aún las del gobierno, muchas veces se mueven por esos mismos intereses. Así, solamente con el control parcial, sobre el rápido influjo de la tecnología en las escuelas, la labor de los educadores es manejarla con atención.
La tecnología aporta capacidades nuevas importantes e interesantes que expanden las opciones de qué y cómo enseñamos. Pero existe otra cara de la moneda. Es muy fácil con el entusiasmo, pasar por alto restricciones y limitaciones de la tecnología que estrechan la visión de las matemáticas y la enseñanza. Por ejemplo, es mucho más económico darle a cada estudiante una calculadora gráfica que ofrecerles acceso equivalente a los computadores. Decidirse por las calculadoras por otro lado, puede estrecharnos la visión de las matemáticas, de lo que se puede lograr en una pantalla con las gráficas y sus descripciones simbólicas. Se puede lograr mucho por esa vía, y las personas razonables pueden decidir que es eso lo que desean lograr en sus programas de matemáticas, aunque también es posible involucrarse tanto con un tipo de método de graficar que otros enfoques y aplicaciones del álgebra se olvidan.
Lo mismo ocurre con la enseñanza. Mientras que algunos maestros disfrutan el experimentar con herramientas nuevas, otros son más creativos cuando su atención no está dividida entre su oficio (estudiantes, pensamiento y contenido del curso) y lo que puede parecerles como detalles tecnológicos de bajo nivel. Para estos maestros, las ventajas de una nueva herramienta (aún cuando acepten que tiene ventajas) puede ser inconveniente por el entrenamiento al que deben someterse para usarla con fluidez. Algunos de los nuevos currículos establecen tanto una visión para el uso de la tecnología como la provisión de recursos para que los maestros ganen habilidad en ella.
¿Qué se debe hacer? Mantenga el cambio bajo control. Ofrezca tiempo y capacitación para que los maestros se conviertan en usuarios creativos de la tecnología de que disponen. Mantenga una visión clara de lo que se quiere obtener de la tecnología, responsable pero no gobernada por los cambios de lo que posibilita la tecnología. Piense principalmente qué es lo que desea para sus estudiantes (las metas particulares del aula y las necesidades de cada estudiante) y después de establecer sus metas, evalúe si las herramientas lo acercan o alejan de ella.
ACERCA DEL AUTOR
El Dr. Godenberg estudió matemáticas, psicología y educación en las Universidades de Brandeis y Harvard. En 30 años de educación en matemáticas, ha estado más de dos décadas en el aula de clase; pasando de su salón de segundo grado hasta los grados superiores; y también por más de dos décadas muy interesado en el tema de la tecnología en la educación matemática. Líder internacionalmente reconocido tanto en educación matemática como el uso de la tecnología en educación, es un Científico Experimentado del Centro para el Desarrollo de la Educación en Newton, Mass. Estados Unidos.
NOTAS DEL EDITOR:
[1] Con Geometric Supposer los estudiantes pueden trabajar simultáneamente en diferentes tipos de figuras, y crear nuevas figuras conectadas con las formas básicas. Pueden mover una figura y ver cómo ese movimiento afecta a las otras, la relación existente entre ellas y sus medidas. http://www.cet.ac.il/math-international/software5.htm
[2] El software Fathom permite al estudiante manejar el modelado de datos matemáticos y estadísticos. Permite explorar datos, graficar funciones y crear simulaciones animadas. Ofrece la posibilidad de ingresar sus propios datos, utilizar los datos de más de 300 archivos que vienen con el programa, importar datos de archivos de texto o descargarlos directamente desde Internet. http://www.keypress.com/fathom/
[3] Un ejemplo de número racional con expresión decimal periódica es 10 ÷ 3 = 3.3333333333333333
[4] "The Teaching Gap", libro escrito por James W. Stigler y James Hiebert. En él los autores afirman que su trabajo es acerca de la enseñanza y cómo mejorarla. Sus sugerencias de mejoramiento provienen de su participación en el "Third International Mathematics, and Science Study (TIMSS)".
[5] "The Third International Mathematics and Science Study (TIMSS) 1999 Video Study" examina diversas practicas de enseñanza en clase y a través de análisis en profundidad de videos de clases de mametmáticas en octavo grado. http://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=2003013 Ver el sitio oficial del "International Study Center" http://timss.bc.edu/
[6] Una programa de calculadora rota, hecho por Garry Clark en MicroMundos Pro, está disponible en la dirección http://www.mathcats.com/microworlds/brokencalculator_overview.html Para ejecutar la calculadora debe instalar previamente en el navegador el "MicroMundos Web Player" y entrar por el enlace "Go to the broken calculator project!". La Isla de las Calculadoras Desechadas es otro sitio con ejemplos de problemas y una calculadora rota en línea: http://www.mste.uiuc.edu/dildine/broken/
CRÉDITOS:
Traducción al español realizada por EDUTEKA del artículo "Thinking (and Talking) About Technology in Math Classrooms" escrito por Paul Goldenberg y publicado por Education Development Center, Inc.
Publicación de este documento en EDUTEKA: Septiembre 6 de 2003.
Última modificación de este documento: Septiembre 6 de 2003.





